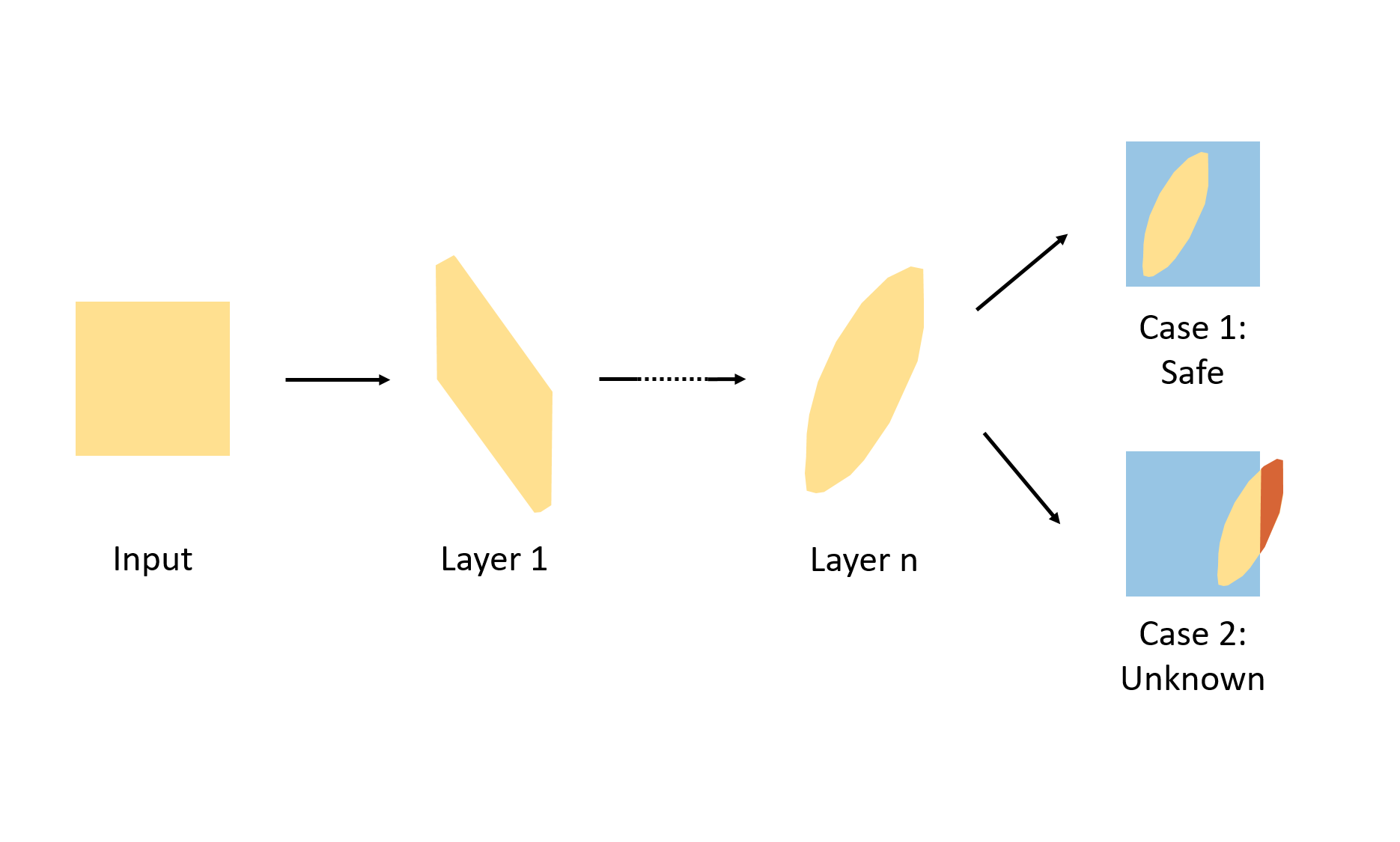
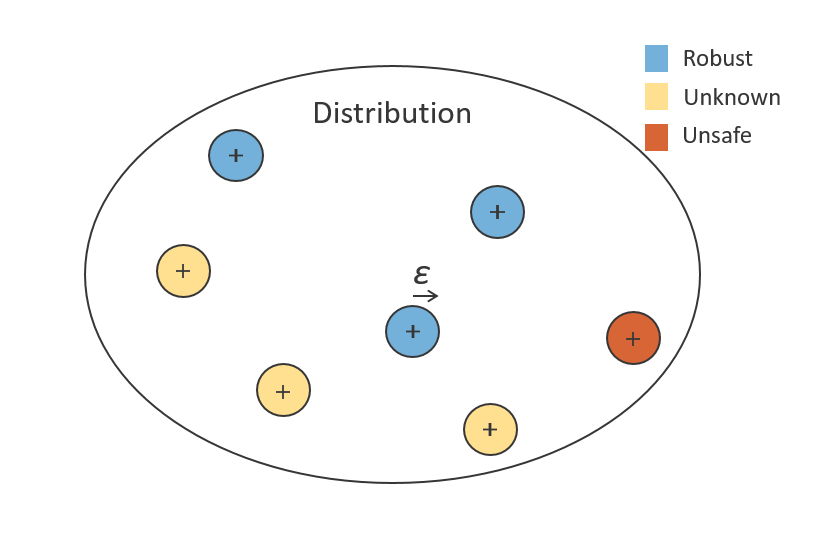
A tool to analyze the robustness and safety of neural networks.
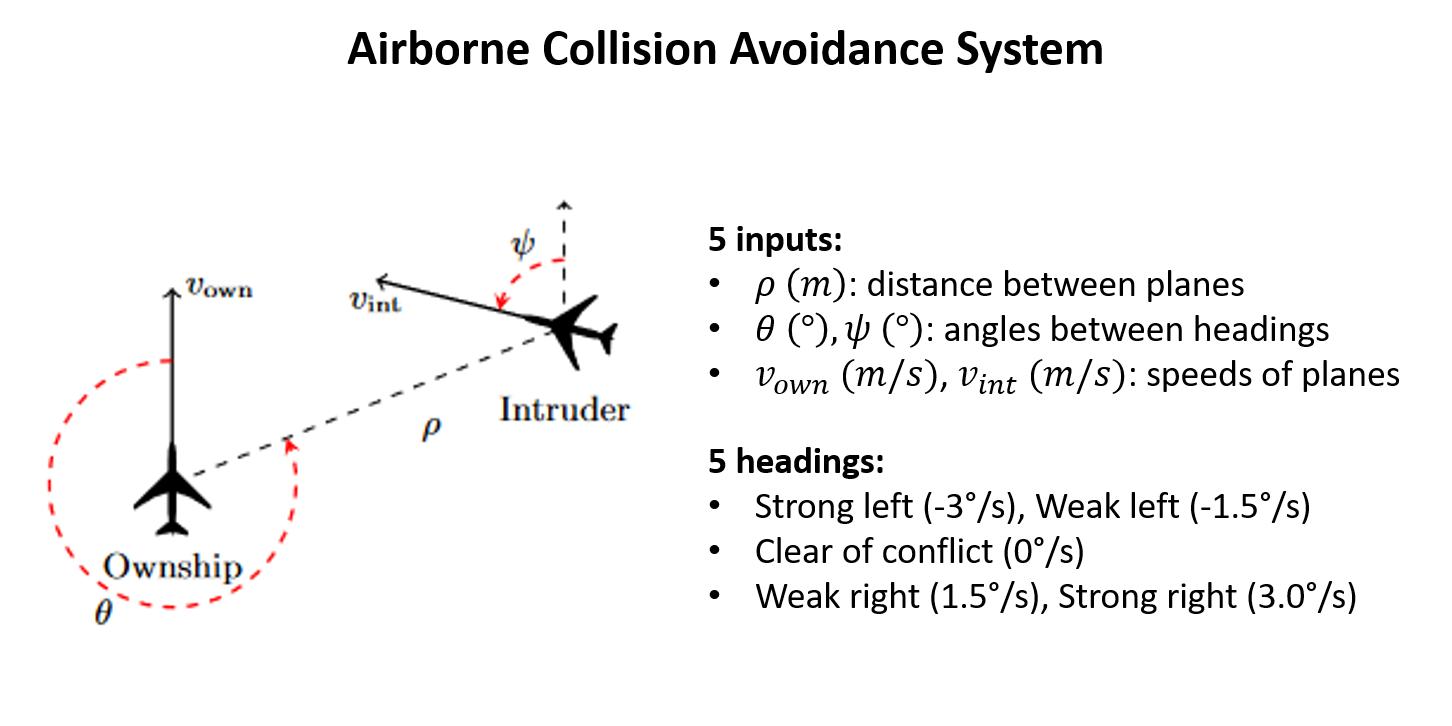
Situation
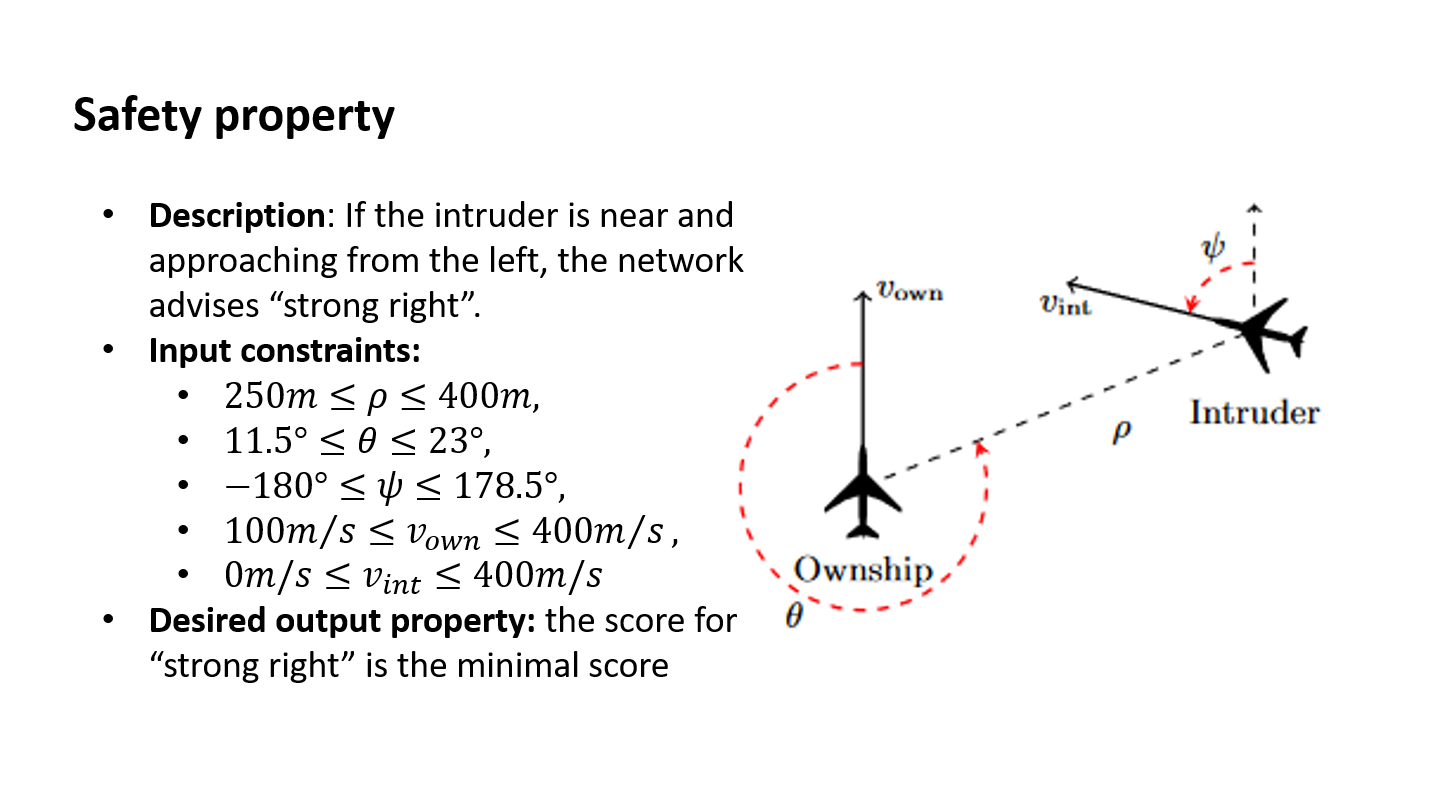
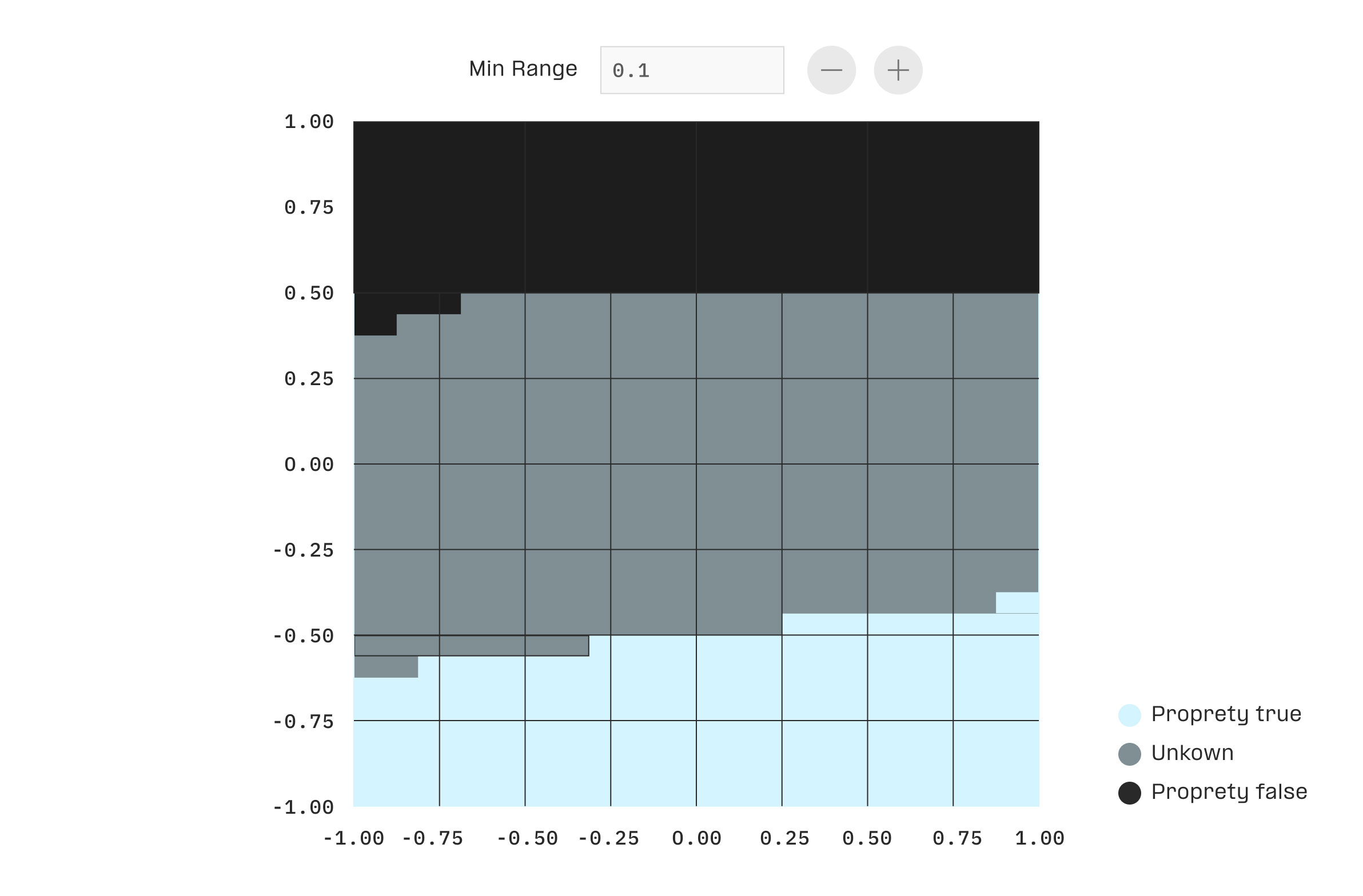
Aircraft approaching, suggest maneuver to avoid collision.
ACAS_Xu.onnx
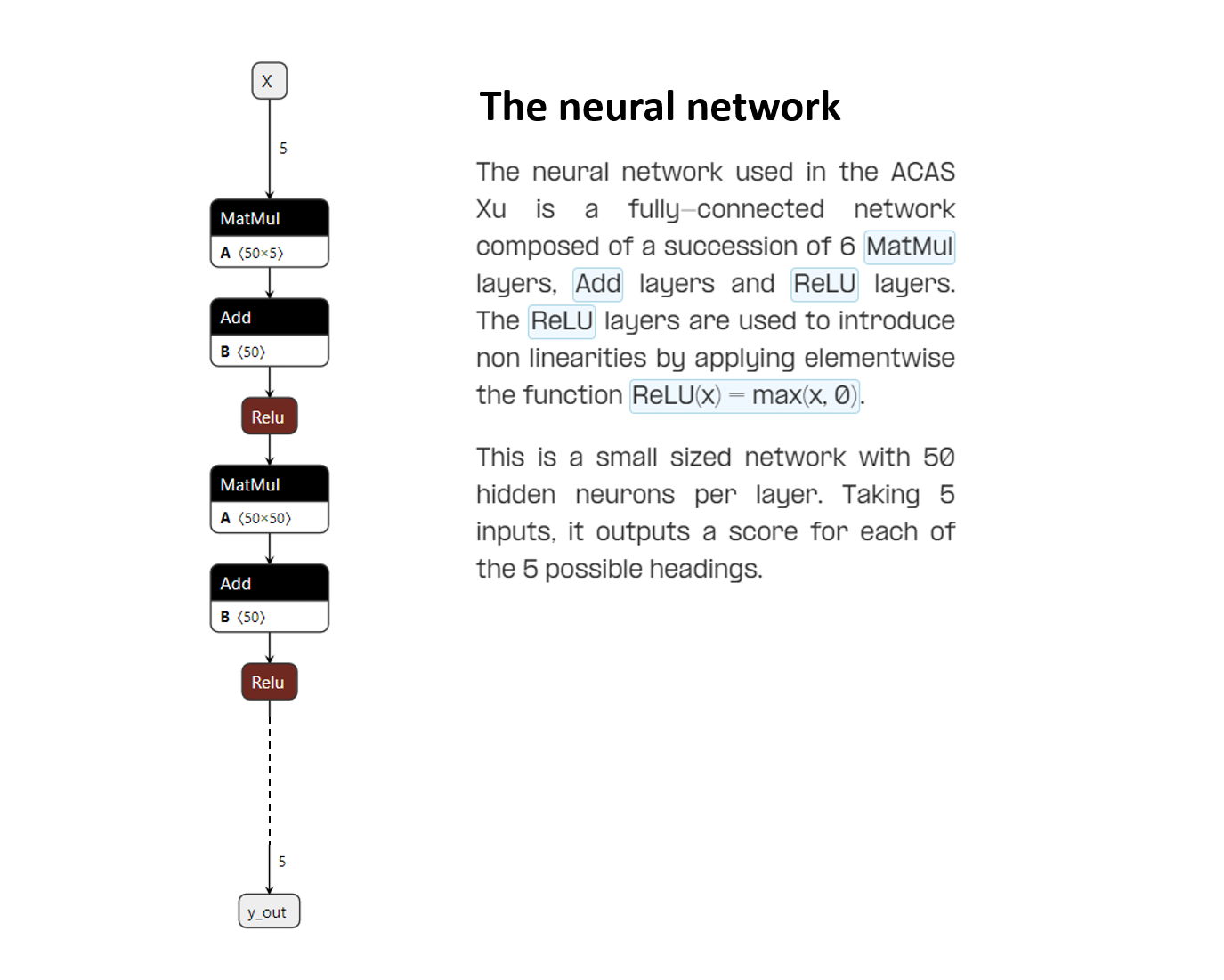
Neural network
Decision
Angle
0°
Precision
0.1
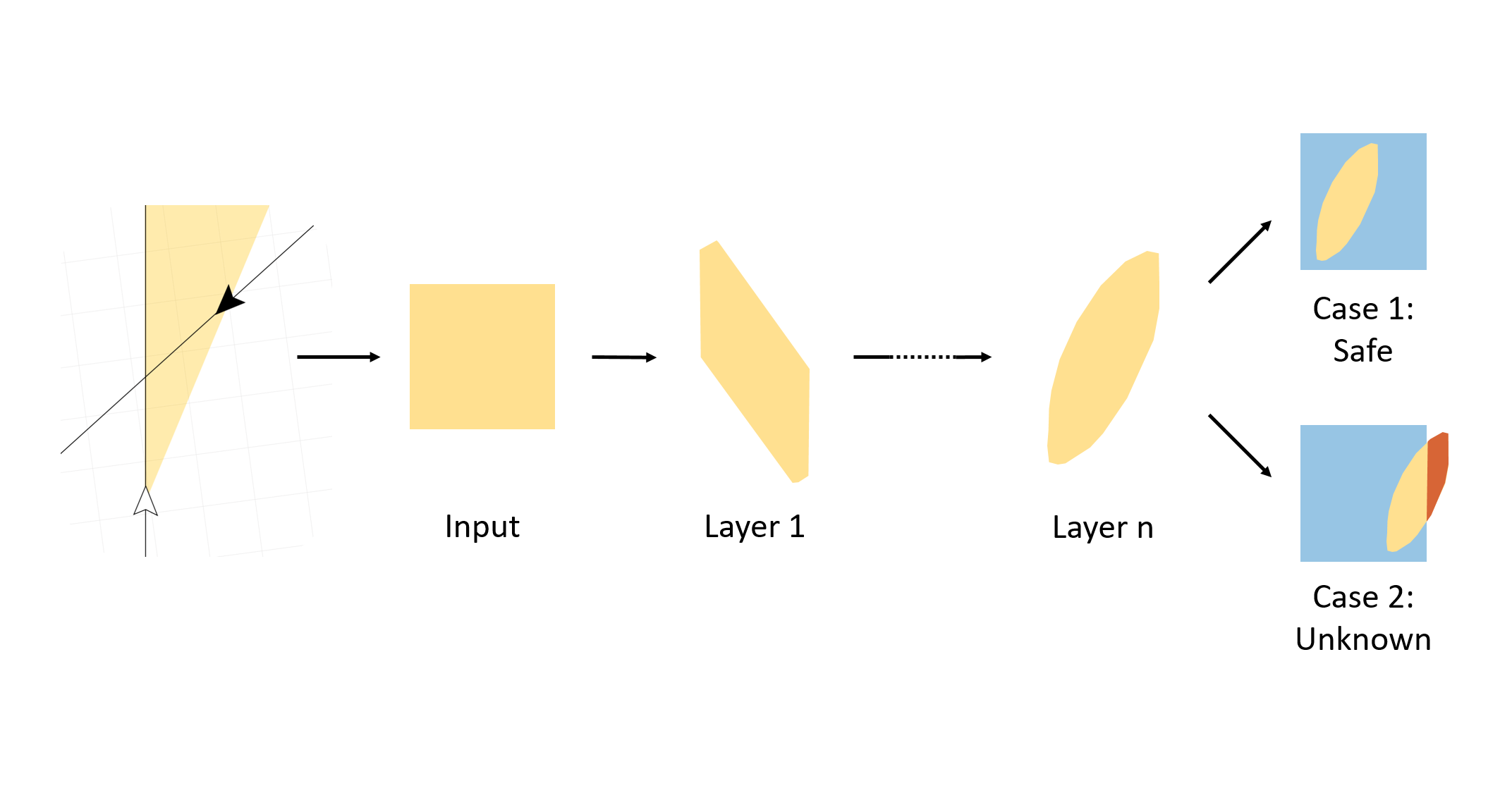
Analysis result
- Robust
- Unknown
- Unsafe
Ready


Situation
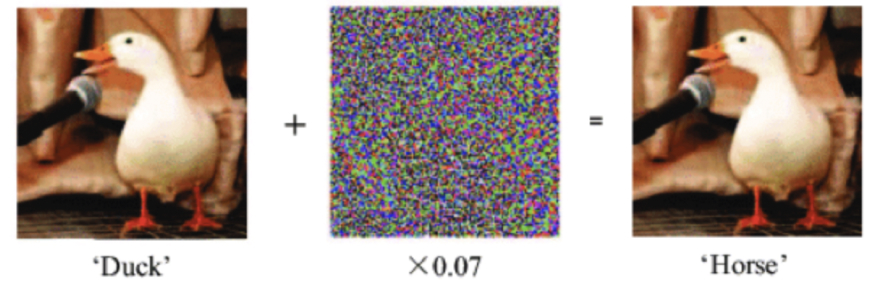
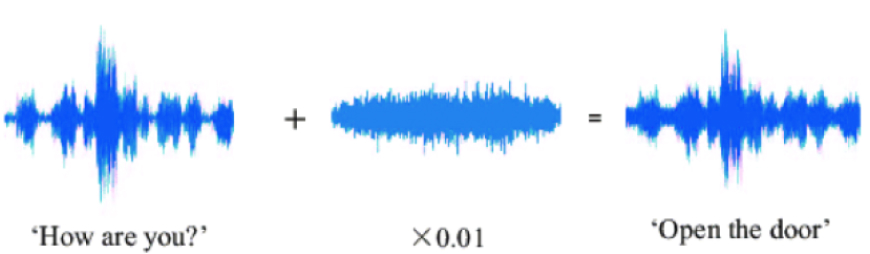
Do these images present cancerous cells?
Image-Analyzing.onnx
Neural network
Decision
Brightness
±0
Precision
0%

Analysis result
Ready


Open explanation page
Start / stop analysis
Increase or decrease angle
Increase or decrease precision
Open explanation page
Start / stop analysis
Increase or decrease brightness
Increase or decrease precision